คณิตศาสตร์ ในชีวิตประจำวันของเรา น่าเสียดายที่เราคุ้นเคยกับการเห็นภาพเนื้องอกและมะเร็งผิวหนัง คุณอาจสังเกตเห็นว่าพวกมันไม่ได้สมมาตรกันทั้งหมด ความไม่สมมาตรนี้มีประโยชน์สำหรับแพทย์ในการวินิจฉัย แต่เหตุใดจึงไม่สมมาตร อ่านต่อ ต้นกำเนิดเลขคณิต ทางชีวภาพเป็นสัญลักษณ์ของการรับรู้ไม่มีที่สิ้นสุด
คณิตศาสตร์ กับการเติบโตของเนื้องอก
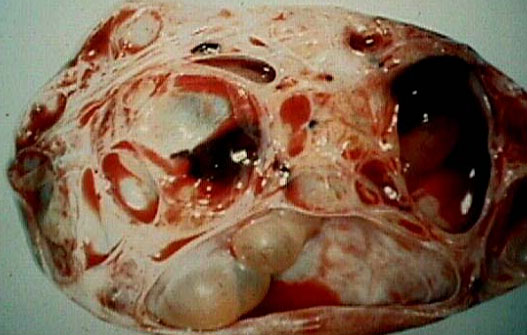
ตามสัญชาตญาณ เราคิดว่าวัตถุสมมาตรมักพบได้ในธรรมชาติ แต่บางที ความไม่สมมาตรอาจพบได้บ่อยกว่านั้นอีก เพื่อให้สิ่งต่าง ๆ ซับซ้อนขึ้น บางครั้งวัตถุเดียวกันอาจมีความสมมาตรและบางครั้งก็ไม่สมมาตร ยกตัวอย่างฟองสบู่ เมื่อพวกมันมีขนาดเล็ก มันดูสมมาตรอย่างสมบูรณ์แบบ แต่เมื่อเราเพิ่มรัศมี เราจะเห็นว่าความสมมาตรนั้นขาดหายไป ฟองสบู่จะไม่กลมสมบูรณ์แบบอีกต่อไป ปรากฏการณ์นี้เกิดจากการมีผลกระทบทางกายภาพ เช่น ลมและแรงโน้มถ่วง ดังนั้นเราอาจยืนยันได้ว่ารูปร่างสุดท้ายของฟองสบู่นั้นเกิดจากปัจจัยหลายประการ และผลกระทบของแต่ละปัจจัยนั้นไม่สามารถละเลยได้
สิ่งเดียวกันนี้เกิดขึ้นกับการเติบโตของมะเร็ง: รูปร่างที่ไม่สมมาตรนั้นเกิดจากปรากฏการณ์ทางชีววิทยาที่แตกต่างกัน เพื่อให้เข้าใจว่าปรากฏการณ์เหล่านั้นคืออะไรยังคงเป็นศูนย์กลางของการวิจัยอย่างต่อเนื่องในสาขาชีววิทยาและการแพทย์ คณิตศาสตร์อาจให้ข้อมูลเชิงลึกที่มีคุณค่าเกี่ยวกับแง่มุมต่างๆ ของการเติบโตของเนื้องอก ด้วยการสร้างแบบจำลองทางคณิตศาสตร์และตรวจ สอบวิธีแก้ปัญหา เราแยกแยะระหว่างแง่มุมต่างๆ ที่เป็นไปได้ในกลไกการเติบโตของเนื้องอก สิ่งนี้อาจเป็นประโยชน์ในการพัฒนาวิธีการรักษาที่มีประสิทธิภาพและการให้ข้อมูลเสริมแก่นักชีววิทยาและแพทย์
- เราจำลองการเติบโตของเนื้องอกได้ไหม
รูปร่างของเนื้องอกเป็นผลมาจากปฏิสัมพันธ์หลายอย่างระหว่างเซลล์เนื้องอก เซลล์ที่มีสุขภาพดี โมเลกุล และเนื้อเยื่ออื่นๆ ในการอธิบายวิวัฒนาการของมันทางคณิตศาสตร์จากมุมมองทั่วโลก เราสามารถใช้ “สมการการแพร่” สมการการแพร่เป็นเครื่องมือทางคณิตศาสตร์ที่ดีในบริบทดังกล่าว เนื่องจากสมการนี้สามารถอธิบายผลกระทบทั่วโลกของกระบวนการทางกายภาพซึ่งเกิดขึ้นในระดับที่เล็กกว่ามากได้
โดยทั่วไป กระบวนการในระดับเล็กคือการแพร่กระจาย: การเคลื่อนที่สุทธิของวัตถุใดๆ (เช่น อะตอมหรือโมเลกุล) จากบริเวณที่มีความเข้มข้นสูงไปยังบริเวณที่มีความเข้มข้นต่ำกว่า ตัวอย่างหนึ่งของพฤติกรรมดังกล่าวอาจเป็นวิวัฒนาการของอุณหภูมิ (หรือความร้อน) ในห้อง จากประสบการณ์ เรารู้แล้วว่าถ้าเราให้ความร้อนแก่ส่วนเล็กๆ ของห้อง ความร้อนจะกระจายไปยังส่วนที่เหลือในไม่ช้า ปัจจุบันนี้เราทราบดีว่าถึงสมดุลทางความร้อนแล้ว เนื่องจากอะตอมและโมเลกุลที่ประกอบเป็นอากาศกำลังเคลื่อนที่แบบสุ่มและไม่เป็นระเบียบ การเคลื่อนไหวนี้เรียกว่าการเคลื่อนไหวแบบบราวเนียน ซึ่งตั้งชื่อตามโรเบิร์ต บราวน์ นักพฤกษศาสตร์ชาวอังกฤษผู้อธิบายการเคลื่อนไหวนี้ครั้งแรกในปี พ.ศ. 2370 ขณะสังเกตการเคลื่อนที่ของอนุภาคละอองเกสรในน้ำ ที่น่าสนใจคือ สมการการแพร่ในคณิตศาสตร์ได้รับการศึกษาอย่างอิสระแล้วตั้งแต่ปี พ.ศ. 2365
- การแพร่กระจายและรูปแบบที่แตกต่างกัน
ไอน์สไตน์บรรยายถึงการแพร่กระจายแบบใดแบบหนึ่ง ซึ่งปัจจุบันเรียกว่า “การแพร่กระจายเชิงเส้น” มีลักษณะเฉพาะคือ “การกระจัดกำลังสองเฉลี่ย” ซึ่งเป็นค่าเฉลี่ยของจำนวนอนุภาคที่เคลื่อนที่ตามเวลา “การกระจัดกำลังสองเฉลี่ย” เป็นแบบเส้นตรงตามเวลา ซึ่งหมายความว่า โดยเฉลี่ยแล้วหากเรารอ 5 หน่วยในเวลา อนุภาคจะเคลื่อนที่ √5 หน่วยในอวกาศ ความเป็นเส้นตรงตรงนี้อยู่ระหว่างปริมาณของเวลากับกำลังสองของปริมาณของปริภูมิ
นี่ไม่ใช่การแพร่กระจายที่เป็นไปได้เพียงอย่างเดียว และมีการใช้และศึกษาประเภทอื่น ๆ การจำแนกประเภทมักขึ้นอยู่กับแนวคิดเรื่อง”การกระจัดกำลังสองเฉลี่ย” ตัวอย่างเช่น ใน “การกระจายตัวยิ่งยวด” อนุภาคได้รับอนุญาตให้ “กระโดด” (ปัจจุบันเรียกว่าการเดินของเลวี) และเพื่อให้เคลื่อนที่ในอวกาศได้มากขึ้น พฤติกรรมนี้ไม่เพียงแต่พบได้ทั่วไปในโมเลกุลเท่านั้น แต่ยังพบได้ในสัตว์อีกด้วย
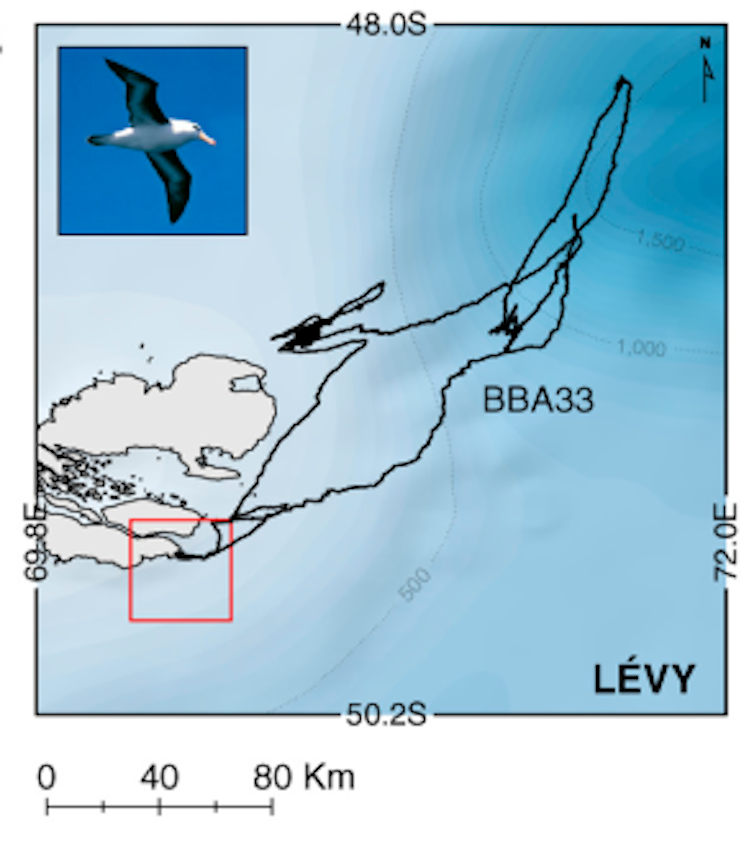
ตัวอย่างเช่น อธิบายกลยุทธ์ การหา อาหารของอัลบาทรอส ได้ดี เราอาจสังเกตเห็นความแตกต่างระหว่างวิถีการเคลื่อนที่ของบราวเนียนกับการเคลื่อนที่ของอัลบาทรอส ในระยะแรกอนุภาคจะอยู่ใกล้กับตำแหน่งเริ่มต้น ในขณะที่อนุภาคอัลบาทรอสจะเคลื่อนที่เป็นระยะไกล (การกระโดดของเลวี)
ข้อดีหลักประการหนึ่งของคณิตศาสตร์ก็คือ บ่อยครั้งสามารถนำเทคนิคและแนวคิดที่คล้ายกันมาปรับใช้เพื่ออธิบายสถานการณ์ที่แตกต่างกันในธรรมชาติได้ นี่เป็นกรณีของสมการพาราโบลาซึ่งเป็นลักษณะทั่วไปของสมการการแพร่ข้างต้น และใช้เพื่อสร้างแบบจำลองปรากฏการณ์ต่างๆ มากมาย เช่น การแกว่งตัวของราคาตลาดหุ้น หรือวิวัฒนาการของวัสดุที่อยู่ระหว่างการเปลี่ยนเฟสสำหรับ ตัวอย่างการละลายน้ำแข็งเป็นน้ำ ลักษณะทั่วไปในปรากฏการณ์ที่อธิบายโดยสมการพาราโบลามักจะเป็นการบรรยายถึงผลกระทบทั่วโลกที่เกิดจากกระบวนการในระดับที่เล็กกว่าเสมอ
- รูปร่างของเนื้องอก
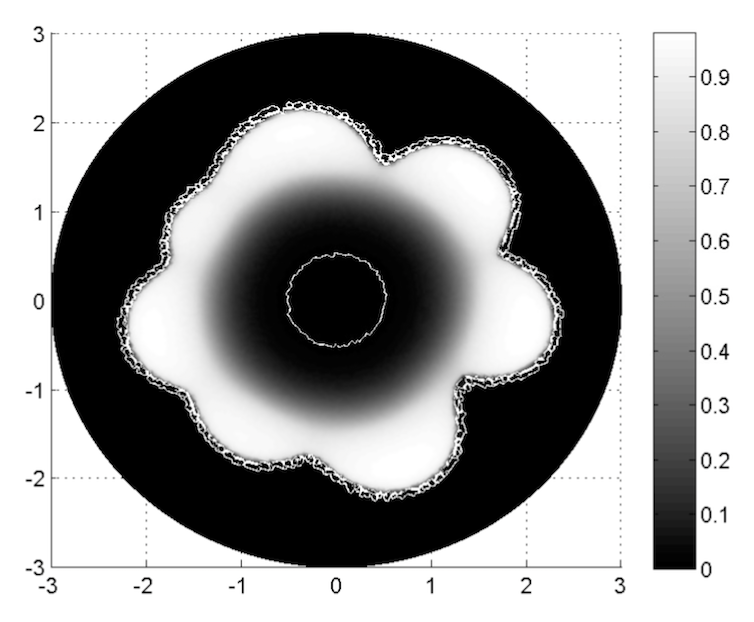
สมมติว่าทุกเซลล์ (มากหรือน้อย) เคลื่อนที่แบบสุ่ม เราอาจอธิบายวิวัฒนาการของความหนาแน่นของเซลล์ในอวกาศ (จำนวนเซลล์ต่อหน่วยปริมาตร) ด้วยสมการการแพร่กระจาย อย่างไรก็ตาม เราจะไม่ได้รับการวิวัฒนาการที่ไม่สมมาตรโดยพิจารณาเฉพาะความหนาแน่นของเซลล์ อันที่จริง คุณลักษณะของสมการการแพร่คือการทำให้วิวัฒนาการมีความสมมาตรมากขึ้น โดยมีผลคล้ายกับสมดุลทางความร้อนที่อธิบายไว้ข้างต้น
เพื่อให้ได้ความไม่สมดุล เราจำเป็นต้องมีองค์ประกอบเพิ่มเติมในแบบจำลอง แต่จะต้องเพิ่มเอฟเฟกต์ใดเข้าไป นี่คือเวลาที่คณิตศาสตร์จะมีประโยชน์ต่อชีววิทยา เนื่องจากนักคณิตศาสตร์อย่างเราๆ สามารถทดสอบสมมติฐานได้ แท้จริงแล้ว การเพิ่มองค์ประกอบต่างๆ ให้กับโมเดล ทำให้สามารถจำลองการเติบโตของเนื้องอกในด้านต่างๆ และเข้าใจกลไกของมันได้ดียิ่งขึ้น องค์ประกอบดังกล่าวอาจเป็น
ตัวอย่างเช่น การมีอยู่ของสารอาหาร (โดยทั่วไปคือออกซิเจนหรือกลูโคสที่มาจากหลอดเลือด) ซึ่งการมีอยู่นั้นถูกจำลองอีกครั้งโดยสมการการแพร่กระจายที่อธิบายว่าเนื้องอกใช้สารอาหารอย่างไร หรือการมีอยู่ของแรงกดดันภายนอกที่ใช้โดยผู้อื่น เนื้อเยื่อ เช่น อวัยวะที่อยู่ด้านหนึ่งของเนื้องอก ด้วยการรวมคุณสมบัติเหล่านี้ไว้ในโมเดล เราจะได้รูปร่างดังในรูปด้านบน ซึ่งใกล้เคียงกับที่เราเห็นในโลกแห่งความเป็นจริงมากขึ้น อ่านต่อ คณิตศาสตร์…ของมะเร็งเต้านม !!!